Curt Herzstark and his Pocket Calculator CURTA.

1st part

(since April 22, 1997)

Last Update: August 05, 2021 -- THE CURTA REFERENCE

backup

6/88 page 5-9

This artice was translated by Andries de Man
http://udel.edu/~ademan

Copies of this article can be purchased from
Charles Babbage Institute at University of Minnesota

May 31, 2006 - Thanks to Jürgen Müller for finding an original
copy of this article and producing much improved scans of the
images. They're a big improvement over my 5th generation
photocopy images! Also see an additional note from Jürgen at
the end of this article about Backup magazine.
-Rick-

My efforts in writing up information about the development of mechanical calculators made me acquainted with Curt Herzstark. He died recently, at October 27, 1988, at the high age of 86. His death has struck me. We still had so much to discuss. But nature takes his course, and all that is left to me are fond memories of the many interesting conversations I had with Curt Herzstark. Another thing left is trying to write down his intellectual heritage. In this sense the present first part of my contribution is also an obituary.

Peter Kradolfer

It started with a letter to Curt Herzstark in April 1988. I asked him if I could drop by, there were some things about the CURTA I was interested in. Only two days later the telephone rang "Yes, please come, I am in good health", which is not obvious at the age of 86. Surprised by such a spontaneity, I took the train to visit him. It was a day which I will not easily forget. "You shouldn't exhaust this man, he surely is of an age at which one needs some rest" was the warning I received from my wife when I left. I intended to return after three hours, at most. But that did not happen. After five hours of the liveliest conversation one can imagine Curt Herzstark stipulated laconically: "Well, we will never be able to finish, but please come back." I accepted this invitation thankfully, so which started as a single visit became a series of meetings. However, we never "finished". It is hard to tell the story of a rich life in only a few days. At first, Curt Herzstark impressed me with his technical achievements. The more I learned about his life, the more I was moved by the misfortunes he had and which he surmounted in his charming but tenacious way. I will tell about our conversations from a personal, i.e. not a historical, viewpoint. It will highlight many interesting details of his life.

Figure 1: Two CURTA models with the serial numbers 4086 (left) and 63122 (right). The elder machine dates from the first production year 1947, the younger at the right was made in 1966, almost at the end of the production time. Despite of a 19 years difference, the two machines are almost the same. [Note by AdM: the left one has cylindrical setting knobs].

Summary

Nowadays a pocket calculator is usually an electronic gadget with more or less sophisticated functions. Few people know that there were already mechanical pocket calculators shortly after the second world war. And only a few collectors of historical calculators know who was the inventor of the most famous and compact mechanical calculator. Curt Herzstark was, next to Konrad Zuse, the only pioneer of mechanical calculators still alive in 1988 [1]. His achievement is unique in two ways. First, he invented the smallest four-function pocket calculator that has ever reached mass production. Second, the patent was granted as early as 1938, but production didn't start until 1947. A concept which is worth entering production nine years after obtaining a patent has to be extremely ingenious! Only the dimensions and weight of the machine are "small" - the CURTA fits easily in one's hand and weighs only a few 100 grams. In contrast, its performance is great. With an accuracy of 11 or 15 positions, the machine is still (1988) more accurate as most modern electronic pocket calculators. And it was also significantly faster than all calculators on the market after the war. Its special construction enabled one to perform a multiplication with the number 9 using only two revolutions of the crank.

Curt Herzstark, the man.

Figure 2: Curt Herzstark in June 1988, photographed during the first Swiss calculator exhibition in Biel.

He was born in 1902 as the son of a businessman in Vienna. Father Herzstark founded in 1905 in Vienna the company "Rechenmaschinenwerk AUSTRIA Herzstark & Co.", which built different varieties of the Thomas-calculators with additional patented Herzstark-inventions. The name "Austria Rechenmaschinen" [2] is well known among collectors of historical calculators. During the first world war the AUSTRIA factories had to make precision parts for shrapnel-fuses and collected by this occasion experiences in "Austauschbau" [3]. In 1916, after the "Realgymnasium" [3a], Curt started an apprenticeship as precision mechanic and toolmaker in the factory of his father. His mentor, Joh. Hayard, came from Glashütte [4], one of the centers of precision mechanics at that time. So Curt Herzstark was lucky to get a very decent education, despite of the war. Most important for his later occupation as an inventor of calculators was getting acquainted with the brand new method of "Austauschbau". After finishing his final test 'with honors' he started studying engineering at the "Höhere Staatsgewerbeschule" in Vienna, which can be compared with the modern swiss "Höhere Technische Lehranstalten" (HTL). Curt Herzstark did internships in his fathers' factory, where he worked in Assembly and Sales. In 1926 he was made responsible for reorganizing sales of Austria products in Czechoslovakia. Things could have proceeded steadily from there-on, but the tremors of world history made that impossible.

In March 1938, Austria was "brought back home" in the Reich by the Nazi's. As a consequence, the German army surveyed the industry of the annexed country [5], so they also examined the Austria-factories. The firm could save its existence by completing very difficult test-orders for the construction of gauges for the Army Supplies Office in Berlin. In other words: the company was not nationalized by the Nazi's, despite of the not purely arian [6] descent of Curt Herzstark, who had been promoted to technical manager in the mean while. In other words, the firm Austria was not nationalized, but had to adapt their production to the wishes of the Nazi's.

Everything went well, until 1943. Germany was already in its fifth year of war and failure after failure emerged: in May 1943 the capitulation of the German-Italian army in Africa, the fall of Mussolini in July, the advance of soviet troops at the eastern front and the American-British bombing offensives at targets in the North and West of Germany are only a few of the main events in this year. Curt Herzstark was arrested. He was accused of "helping Jews and subversive elements" and "indecent contacts with arian women". The only accusation they could hold against him was that employees, who were not at all inclined to racism, were caught at listening to broadcasts of the enemy (the English) and he tried to defend them. One of the accused was executed. When he was called as a witness in this case, Curt Herzstark didn't return home. Without any due process he was sent to Vienna in "preventive custody", as such an injustice was cynically called. After that he was put in a prison for Jews and finally deported to Prague, to the infamous Pankraz prison. Here he was taken over by the SS. Curt Herzstark told me things about the treatment in Prague that shocked me. I was very distressed by all the cruelties and the acts of contempt intelligent human being executed at that time. Curt Herzstark told me literally: "People tell a lot; I tell you only what I experienced myself", and he went on: "And I was even lucky, I went to Buchenwald" [7]. I startled, because I knew Buchenwald, and I knew that ten-thousands had died there. So in the fall of 1943 Herzstark was brought to the concentration camp Buchenwald "for special application". The reports of the army about the precision-production of the firm Austria and especially about the knowledge of Herzstark lead the Nazi's to treat Herzstark as an "intelligence-slave". Brought to the edge of desperation in the "small camp", he was allowed to move to the "large camp" at the end of 1943 and was called to work in the Gustloff factory [8] linked to the concentration camp. The name "Gustloff-Factories" was used for expropriated companies in Nazi Germany. There were many of those factories in Germany and they all worked for the military. The Gustloff factory of the Buchenwald used experienced workers that were transferred there from all over Europe. Generally speaking they were not Jewish. Soon Herzstark got special control tasks which he exercised - whenever possible - in the interests of his fellow prisoners; this put him at rather high personal risks. Apart from the manufacture of items for the military, there were also occasions of war loot repair. For example, after the retreat of the Germans from Italy in the summer of 1944, several truckloads of Olivetti manufacturing machines were transported to Buchenwald. Herzstark was ordered to prepare them for use. After that, the Thüringer manufacturers were invited to stock up with cheap production machines. Herzstark had to present them to the customers. He recognized one of them as the well-known "Waffen-Walther" [Arms-Walther], who was also famous for constructing of the "Walther Universal Calculator". [9]

Figure 3: Detailed view of the central driving element of the CURTA, the so-called complemented stepped drum. Original size about 2 x 2.5 x 4 cm.

The CURTA Calculator

Curt Herzstark got the idea for the construction of a four-function pocket calculator from remarks made by customers during his sales travels. Additionally, there was a need to find a product that would in the long term enable the AUSTRIA company to survive independent from suppliers. There existed pocket calculators [10], but they were only able to do additions and subtractions. For all calculators two main problems had to be solved - the driving mechanism and the carrying of tens. Both of them were solved for Herzstarks machine in a unique and original way. We will return to this later (see Figure 3).

Figure 4: Three prototypes of the CURTA from the 1940's, photographed in Curt Herzstarks home in April 1988.

In the winter of 1937/1938, after years of tinkering, the construction of the four-function calculator was essentially completed, and a first prototype was built and working (see Figure 4, Machine 1, at the far right). Two inventions - the complemented stepped drum and reduction gear - were filed for patent shortly after the Nazis took over power in Austria in 1938. Two patents were granted under DRP [11] No. 747073 and 747074, but no production was started; from the summer of 1938 on the AUSTRIA factories had to make measuring devices for the German army. On the other hand, Curt Herzstark didn't want to make his invention public for reasons of competition.

At first, his stay in the concentration camp Buchenwald seriously inflicted Herzstarks health. His condition improved after he could work in the Gustloff factories at the end of 1943. To his surprise the camp commander was already informed about his work on a calculator. He was ordered to make a drawing of the construction. They wanted to give the machine to the Fuhrer after the successful end of the war! That didn't work out. Anyway, Herzstark got access to a small drawing board and drafting machine and worked every spare minute, also on Sunday, at the drawings. Until the liberation in 1945 he had redrawn the complete construction from memory.

During one of my visits to Curt Herzstark I asked him about the origin of the name CURTA. I knew that early drawings showed the name LILIPUT. He told the following:

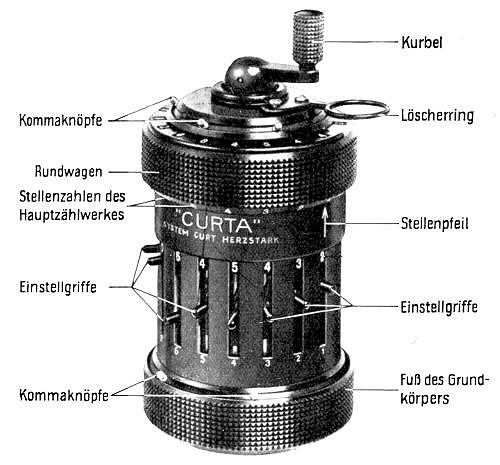
Liliput was indeed the original name, but the Society didn't like it. During the trade fair in Basel (1948) Miss Ramaker, trade correspondent of Contina AG said: "This machine is the daughter of Mister Herzstark. When the father is called CURT, the daughter has to be called CURTA." That's why the machine has been called CURTA ever since.

I went too fast. We have the idea and the name, but yet no machine. Curt Herzstark was still in Buchenwald. It was 1944, and the Allies threatened the German Reich more and more. On August 18, 1944, the Gustloff Factories were bombed, several hundreds of prisoners died and half the factory was destroyed. During the second bombardment a fellow prisoner lying next to him was deadly injured by a bomb fragment. Curt Herzstark survived miraculously. The part of the factory that was still operable was moved to a deserted salt mine in Billroda, 30 kilometers from camp Buchenwald. Here, 600 meters below the surface, they tried to resume production. Two days before the liberation the prisoners walked back to Buchenwald. Finally, the Americans liberated camp Buchenwald on April 11, 1945.

Curt Herzstark was alive and free. Additionally, he had a complete set of construction drawings for his miniature calculator in his pocket. Now the time had come to find a way to realize it. He contacted the Rheinmetall factories. And, as a kind of compensation, Herzstark was named director of the Rheinmetall factories and had to supervise the reconstruction. His fortune didn't last long, because in July 1945 Thüringen and Sachsen became part of the Soviet occupation zone, based on the Potsdam agreement. The few months until November 1945 were sufficient to revise the drawings and make three prototypes. These three prototypes still exist (see Figure 4).

The Soviets started to rebuild their parts of Germany according to their own plans. As a consequence, Curt Herzstark fled to Vienna, where he contacted a friend of the Herzstark family, the Swiss office machine manufacturer Jost. The take-over of production by Jost was almost established - imagine: CURTA, made in Switzerland - when the Principality of Liechtenstein showed up. Prince Franz Josef II of Liechtenstein [12] was trying to convert his poor farming country into a modern industrial state. And he succeeded, as one could read in the press at the anniversary of his government in 1988. The royal family invited Herzstark to build a factory for the production of his calculator in Mauren. It was a tempting offer, and so the Contina AG was founded in 1946. This development was a disappointment for the firm Jost, which was only partially compensated by getting sole representation for the CURTA. Curt Herzstark became technical director of the Contina AG. The real driving force and decision maker of the enterprise was a financing society. One could expect problems due to this difficult and obscure organization structure, and they emerged soon. At first, Curt Herzstark succeeded in manufacturing the first CURTA machines with a team of innovative expert mechanics [13]. The first production hall in 1947 was only provisionary, a ballroom in Hotel Hirschen in Mauren. At the same time production was started, a new factory building was being constructed for the Contina AG. One can easily compare the current building (Figure 5) with the factory from the 50's. A figure in the brochure "Calculation examples for the CURTA calculator", printed around 1955, shows on page 51 a picture of the "CONTINA FACTORY IN MAUREN; PRINCIPALITY OF LIECHTENSTEIN".

Figure 5: Current state of the former factory building of the CONTINA AG in Mauren, FL. Nowadays the building is possessed by Hilti AG.

The first CURTA calculators were of a model with 8 x 6 x 11 positions; in 1954 model II with 11 x 8 x 15 positions [14] was added. The lack of technical expertise in the Financing Society, mentioned before, lead soon to a separation between the Contina AG and the inventor Herzstark. The AG was ended and its shares, so also the part owned by Herzstark, lost their value.

Figure 6: Detail view of a cut-away model of a CURTA I. The ruler below is divided in centimeters.

He was told that he could buy shares in a new AG that had to be established. But how could he pay ? Curt Herzstark didn't have any capital ! Herzstark was able to prevent the loss of his patents with the help of a distinguished Swiss patent lawyer. The patents were still on his name and not assigned to the Contina AG. Herzstark stepped back as technical director in 1951, and became a free-lance employee for some time. The end is easily sketched: The CONTINA AG was bought by the company Hilti in 1966, and the production of calculators was stopped in 1972. Until that date 80,000 CURTA I's and somewhat more than 61,000 CURTA II's had been made. I will explain the differences in construction in the second part.

So far about the story of Curt Herzstark, that was inseparably linked to the CURTA calculator. Many things of the life of Curt Herzstark fascinate me. One of them is the fact that I could speak personally with someone who had been in a concentration camp. For me, a Swiss who was 7 years old at the end of the war, this was an experience that made me experience a part of world history for the first time. But it is also the personality of the inventor. When I first visited Herzstark I was awed by my respect for him. I loosened up during later visits, and we became friends. On September 29, 1988, my last visit to Curt Herzstark, he said: "... you have to preserve my intellectual heritage...". Then there was his modesty. He told exciting stories about the old days, but he never put his achievements first. At first I believed that such an important person had to be wealthy. Wrong. Already during our first telephone conversation he said: "You will see I live modestly." That was true. Much later I tried to find out what was the cause of this. There seems to be only one: the fate of the inventor. The inventor has good ideas, but making money with them - that is done by others!

What's next

A second part, to appear in one of the next issues, will deal with the construction and functioning of the CURTA. Details of the CURTA I will be shown and explained with photo's and drawings. We will also hear from the mechanics A. Kessler and H. Künzli.

Notes:

1: Curt Herzstark, born at January 26, 1902 in Vienna, deceased at October 27, 1988 in Nendeln, Principality of Liechtenstein; Conrad Zuse, born at June 22, 1910 in Berlin [addition AdM: died in December 1995 in Berlin]
2: The Austria-machine is a four-function calculator working with a stepped drum. About 7000 of them were built from 1906 to 1914. They were made in three sizes: with 14, 18 and 22-digit result counters. The stepped drum goes back to Leibniz (1671) and has been applied in large numbers since 1821, instigated by the French insurance salesman C.X. Thomas. The term "Thomas-Calculator" is often used as a synonym for stepped-drum calculator.
3: "Austauschbau" is the manufacturing process with small tolerances that is usually called "Normbau" nowadays. Each part has to be made so accurately that it can be built in any specimen of the machine being assembled without any modifications. In the old days, part that didn't fit were adjusted during assembly. A very nice description of the difficulties caused by this early method can be found in Volume V of the "Schriften des Braunschweigischen Hochschulbundes e.V.: " E.E. Wiberg, Die Leibniz'sche Rechenmaschine und die Julius Universität in Helmstedt: Braunschweig 1977.
3a: [AdM: high school]
4: Glashütte in Sachsen, nowadays GDR. Glashütte is a symbol for the most famous names in the calculator industry, e.g. Burkhardt, Saxonia and Vereinigte Glashuetter Rechenmaschinenfabrik.
5: The Austrian 'states' were abolished, and seven "Reichsgaue" [districts] were formed.
6: Herzstarks father was a liberal Jew, his mother was arian, Curt Herzstark was raised evangelically.
7: Buchenwald was a nazi concentration camp on the Ettersberg near Weimar; from 1937 to 1945 about 240000 people were transported there from 32 nations; about 56000 of them died; nowadays Buchenwald is a memorial and lies in the GDR.
8: Wilhelm Gustloff was the name of the 'Landesleiter' of the NSDAP in Switzerland who was killed in Davos in early 1936. It looks like the expropriated factories were renamed "Gustloff-Factories" in his memory.
9: The Walther "Universal Calculator" is a four-function pin-wheel machine.
10: See also: P. Kradolfer: Einige Rosinen aus der Entwicklung der Rechenmaschinen, Part 3; page 13.
11: DRP Deutsches Reichspatent: The name "Deutsches Reich" was used for Germany from 1871 to 1945.
12: Franz Josef II celebrated his 50th anniversary as Liechtensteins head of state in 1988.
13: Existing, among others, of the Swiss precision mechanics Arnold Kessler and Hans Künzli, who both like to tell about the old days (see Part 2).
14: The shorthand notation 8 x 6 x 11 indicates 8 positions in the setting register, 6 positions in the revolution counter, and 11 in the result counter; The CURTA II has 11 x 8 x 15. Both cases represent a large capacity, taking into account the low weight of 300 gram.

Curt Herzstark and his pocket calculator CURTA

Second part: Construction and functioning of the CURTA

backup

1/89 page 41-45

I have received no education in mechanics, and can not go into all details of the precision mechanical miracle CURTA, and I don't want to. Much of what I will tell will be imprecise or incomplete. However, the ideas of Herzstark and his constructors are so brilliant that they not only fascinate me but also, I hope, many readers. So I'll try to describe the CURTA technically as a layman for laymen - to the memory of the recently deceased Curt Herzstark.

Peter Kradolfer [1]

Summary

The second part of the current contribution "Curt Herzstark and his pocket calculator CURTA" deals with an examination of the constructive principles of this machine. The driving mechanism is the first problem to be solved for mechanical machines. His solution, the complemented stepped drum, will be described extensively. A sketch of the solution of the second main problem, the tens-carrying, has to be abandoned because of space limitations. Instead, the question of the patented ideas will be elaborated, followed by explanations of the constructive changes over time. Technical problems from the early days will be discussed by co-workers of the first hour.
Because of place limitations, part of this will appear in backup 2/89.

Figure 1: CURTA I in its original form with round setting knobs. The machine has serial number 4086, built in 1947 or 1948. At the right the carriage is shown - the blank part corresponds to the 6 digit revolution counter, the dark part to the 11 digit result register. The CURTA is the smallest mechanical calculator for the basic four arithmetic operations that has ever been manufactured in large quantities.

In General

Already in the first part [2] I mentioned that the driving mechanism and the tens-carrying have been two central problems of the construction of calculators for decades. With driving mechanism I do not refer to the operating parts that can be seen on the outside, like the crank and setting levers or keys, but the basic construction principle for performing calculations. Until 1947, all mechanical calculators that had been manufactured in large numbers were, with a few exceptions, either based on the stepped drum (traced back to Leibniz) or on the pin-wheel (introduced by Odhner). [3] Curt Herzstark invented something new: the complemented stepped drum.

Figure 2: A detail of a classical stepped drum machine. Clearly shown are four stepped drums driving gears that are used to set numbers (increasing from left to right). In the original construction shown here the setting gears are shifted by slides. The picture shows a SAXONIA with serial number 1283, a specimen that could date back to 1898.

This term needs an explanation of two points. "Complemented" indicates an algorithm that turns a subtraction into an addition. In other words: instead of a subtraction 481-247 the addition 481+x has to be performed (see text box). "Stepped drum" means a cylindrical driving element with protruding ribs of various lengths (see Figure 2).

The inventor Curt Herzstark has combined both ideas in a unique way in his CURTA calculator. The questions "What is the complement addition good for ?" and "How was it done in the CURTA ?" will be answered next.

What is complement addition, and what is it good for ?

An addition is always simpler than a subtraction, with respect to general carrying-over. I just state this to be so. To prove it, the reader should perform a simple experiment, calculating in his mind or on paper: 189+17=? and 207-18=? Which one is easier ? When I asked several people to do these exercises, they all answered spontaneously that the addition was easier. This was also my own experience. I think that the explanation for it is simple. In the first exercise a carrying into the positive has to be made; in the second one into the negative, and that is usually more difficult. That is why most calculator constructors since Schickard and Pascal [4] tried to build machines that could not only perform direct additions, but also direct subtractions. Extremely important, and hard to realize technically, was tens-carrying until the last digit for both operations.

How does one convert a subtraction into an addition ? The "complement addition" algorithm is based on the addition of the nines-complement of the subtrahend. The example in the text box explains this.

219875 - 5789 = ?
We assume that we have an 11-digit machine.
So the minuend is:	00 000 219 875	Line 1
and the subtrahend is:	00 000 005 789
The nines-complement of the second number is:	99 999 994 210	Line 3
It is made by completing each digit to 9.
Now we add line 1 and line 3:	100 000 214 085
The leading 1 lies outside the range of 11 digits, and is omitted.
The result is 1 short, so we add 1 and get:	00 000 214 086
The right result!

When I heard from this method for the first time, I was amazed that it worked. I have learned to appreciate the importance of the complement addition more and more - the subtraction in modern computers works in the same way. The only difference is that computers work in a binary system, so only with the set {0,1}. Mechanical calculators are based on the decimal system we are more comfortable with, having a set {0,1,2,3,4,5,6,7,8,9} of rank 10. During one of our conversations Curt Herzstark said about the complement addition of the CURTA: "The subtraction by the CURTA is kind of fake, it doesn't subtract at all, it only adds. The trick works, and that's what is important."

Figure 3: Detail of a complemented stepped drum as invented by Herzstark. The strips are about 0.6 mm thick, the total height of the part is 27 mm, with a diameter of 24 mm.

The method can be explained with a number circle but can also be proven mathematically. [5] In the following, we will focus on the technical realization of the idea.

How was the complement addition realized in the CURTA ?

For a description of the construction, I use a paper of Professor Karl Holecek, who taught precision mechanics at the Technical University in Vienna. He wrote in 1950 [5] (cited from [2]):

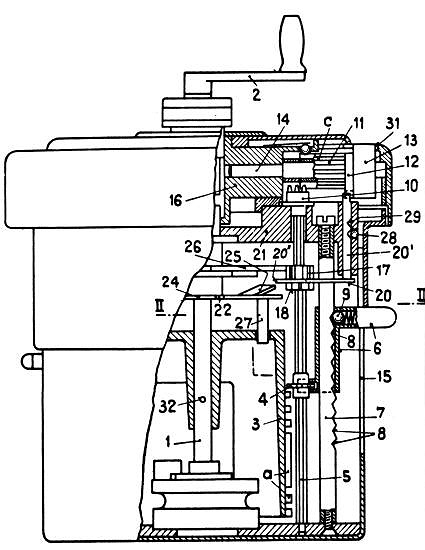
"A calculator will automatically subtract by addition, when it doesn't transfer to the main counter the number set to subtract, but, instead, its nine's complement and subsequently adds a one to the lowest position. The construction problem is to enable a choice between two toothed structures to be used. The smallness of the available space and the expected lack of reliability prevented the use of movable teeth.
The solution was a simple construction, consisting of a rigid body unifying two normal stepped drums, one of which is put upside-down."

Figure 4: Drawing of the functioning of Herzstark's complemented stepped drum, as shown often in the calculator literature of the fifties. [after 3, p.59].

Figure 2 shows the traditional stepped drum and Figure 3 and 4 the complemented stepped drum of the CURTA and its functioning. To understand the mode of operation, I once again cite Professor Holecek [2]:

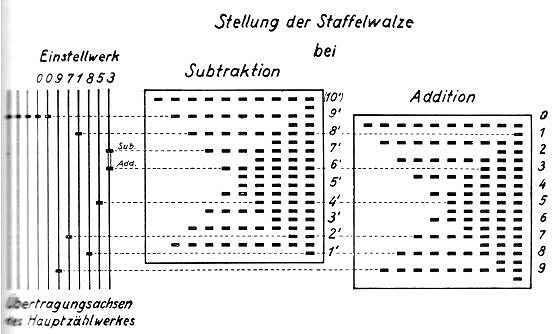
"The one set of teeth, used for additions, starts, like any ordinary stepped drum, at the top with one tooth and ends at the bottom with nine teeth. These tooth segments are designated with 1 to 9 in the right part of Figure 4. Of course, their distance in a vertical direction is equal to the distance the setting gears travel when shifted one unit. The second group of teeth - the complement-toothing - is mixed in with the first in such a way that one and a half times the distance between segments below each segment of the normal toothing, there is a segment of the complement-toothing which adds up with the first one to nine. This system allows one to subtract the set number by simply pulling up, using the crank, the stepped drum over one and a half times the distance between segments, and then turning it in the same direction as for addition. During this operation the 11-digit nine's complement is automatically added, and the first position is increased by one."

Figure 5 [?] shows the details.

Figure 5: At left, an early 11-digit CURTA I (nr. 4086, ca. 1947) with the crank pulled up into the position for subtraction, and at the right a later CURTA I (nr. 63122, ca. 1966) with the crank in the position for addition. The vertical displacement is only about 3 mm.

Holecek continues: "The complement segments are not in operation during addition, because they move between the possible positions of the setting gears. When the stepped drum is shifted up over one and a half times the distance between the segments (Figure 4, center), then the complemented toothing engages with the setting gears, and each gear of the setting mechanism does not rotate over the number of teeth corresponding to the number set, but over its nine's complement. In Figure 4 one can see this for the number 971853. The center of the Figure shows the stepped drum in its position for subtraction. The toothed segments of the complemented toothing are designated with 1' to 9'.

In order to transfer the complete 11-digit nine's complement for the subtraction, nine has to be added to each of the three foremost positions, since they do not engage with the setting mechanism. For this purpose the three foremost shafts have fixed gears in the zero position, that are engaged by the 9 tooth segment 9' in case of subtraction. This way the 11-digit nine's complement is truly added if the stepped drum is in its upper position."

As shown in the box, subtraction needs, apart from adding the nine's complement, also an increment of the lowest position with 1. For this purpose, the shaft at the first position is provided with a second setting gear. Before we go into details, we would like to discuss which advantages the described construction has.

Advantages of the complemented stepped drum when calculating with a CURTA.

Figure 6: Definitions of the most important operating parts of the CURTA (reproduced from [3, p.56]) Before my first visit to Curt Herzstark in April, 1988, I learned how to operate the machine on my way in the train. I expected that Herzstark would ask me about it. Indeed, soon he asked: "Do you know fast multiplication ?" Thanks to my exercises I could affirm this question. To be able to do that, I had studied the manual, a single folded sheet [6] with instructions for the basic operations. From this manual I take the following example, to show the advantages of fast multiplication. For the definitions used, see Figure 6.

133 x 89 = ?

Machine ready, i.e. all counters reset and the carriage in position 1.
Set the number 133 using the setting knobs.
Pull up the crank and make one subtractive revolution, which calculates 133 x (-1).
Set carriage in position 2, experienced users can do that with their left hand.
With pulled-up crank, make 1 subtractive revolution, which calculates 133 x (-10).
Set carriage in position 3.
Push crank back in the position for addition and make 1 additive revolution, which calculates 133 x 100.

A check is provided by the revolution counter, which shows 89, so we did multiply 133 with 89. The result 11837 can be read in the result counter. How can we explain this correct result ? We have calculated: 133 x (-11+100) and that is equal to 133 x 89. We have done it with 3 revolutions instead of 17.

Someone reproducing this algorithm for the first time might find it rather complicated. It would be much easier to crank until ... well, until you make an error. The more I crank, the sooner I turn one revolution too many or too less. Of course one can correct this without any problem. But one has to see the error first. In practice, I just crank until the number 89 shows up in the revolution counter (see Figure 1), without having to think if one needs an additive or subtractive revolution - I watch the revolution counter and always switch modes at the right time. This is an essential difference between the operation of a CURTA and any other hand-driven calculator. Before I wrote down this sentence, I tried to do the same operation - 133 x 89 - on one of my other mechanical calculators, using the method of progressing complement addition. With my TIM [7] I can also, instead of 133 x 89, calculate 133 x (-11+100), the result is the same. The big difference is that, after the calculation, the revolution counter shows 111 instead of 89. The numbers of the tens and units are red, but is not of that much use to get the right multiplicand 89. This is especially important in chain multiplications, like for instance 38 x 14 x 67 x 63.44=?

Figure 7: Cut-away drawing of the CURTA from the Swiss patent application nr. 267995 from August 1, 1950. An almost identical version is shown in the patent DRP 747074 from 1939.

During the production era of the CURTA, i.e. from 1947 to 1970 [8] CURTA's were accompanied by a little pamphlet "Rechenbeispiele für die CURTA" [Examples for the CURTA]. It contained many other examples. It is an exciting passtime for any modern amateur of mechanical calculators to (re)discover the finesses of its practical application. The pamphlet shows practical applications in the fields of trade and industry, statistics, engineering and geodesy. Geodesy or surveying has always been an important application field for various methods of calculation. Alas, I can't go into details about this, I only mention the calculation of arithmetical averages and standard deviations.

The CURTA patents

One exciting task during my CURTA research was to find out which parts of the machine were patented. From my point of view the smallness of the machine would already be worth patenting. Looking at the two first patents, DRP 747073 1938 and DRP 747074 1939, we see that there are other rules for granting patents. A protection by patent has to be limited to the innovation of the product. Although "Smallness" was something new, it was clearly not worth protecting, since it was not sufficiently innovative.

Let's look at the original patent applications. Or better, the two mentioned before, because there are more than 30 (!) patent applications in 14 countries in the name of Curt Herzstark that have something to do with the CURTA. So I will limit myself.

The first one, DRP 747073, valid since August 19, 1938, reads under the heading "Claims":
"Calculator with one single stepped drum and a mechanism for performing subtractions with changing the direction of revolution of the stepped drum, characterized by establishing onto the stepped drum, apart from the normal stepped toothing, a second rigid complemented toothing, in such a way that by an axial displacement of the stepped drum the normal toothing or the complemented toothing can be brought into engagement with the setting gears." This long sentence, which summarizes the claims very well, is followed by three sections completing and detailing on the claims. So we have seen that the first patent relates to the complemented stepped drum, without mentioning this term explicitly. The second patent, like the first one granted in Vienna, but designated DRP [9] and "decorated" with the German eagle and a swastika due to the changed political conditions, protects the transmission gears.

Figure 8: Cut-away model of a CURTA I, upper part. At the right one sees a part of the result counting mechanism with the star of springs pushing steel balls with a diameter of only 2 mm to prevent the horizontal numeral dials from turning to far. The crown gear shaped upper ends of the transmission members, driving the numeral dials at an angle, are seen below. They were a very special technical problem.

Figure 9: Details of the driving section. In the center one sees the complemented stepped drum. Above that sits the tens-bell and the spring of the counting mechanism. At the upper part of the stepped drum the teeth of the revolution counter can be seen. In front of that, a driving member with tens-carrying gear at the top and below a setting slide, which shifts, by means of a fork, the setting gears into engagement with the stepped drum.

Figure 10: A detached carriage, photographed from the bottom. Visible are the horizontally mounted numeral dials and the star-shaped counter body. The two numeral dials at the bottom right each show a pin, which is used in carrying tens. This pin has a diameter of about 0.8 mm. For a number of dials, depending on its position, the pins had to be ground away to half its length. The pin slides, by means of an intermediate part, the so called tens lever, the tens carrying gear down within reach of the ten tooth that is mounted above the stepped drum.

Figure 11: Two zeroizing plates, at the left one from the 15-digit CURTA II, at the right one from the 11-digit CURTA I. Clearly visible are the curved tooth racks with an outer and and inner tooth ring. This construction makes it possible to zeroize the revolution counter or the result counter ad libitum. This is necessary because many calculations require the conservation of intermediate results.

I cite the first line of the claims: "Calculator with only one stepped drum and with setting and counting members arranged in a circle around it, characterized this way, that the transmission mechanism between the setting gears (4) and numeral dials (13) has a gear (10,11), which extends the time of engagement of the stepped drum with the setting gears, thus distributing the friction of the counter members over an as large as possible movement of the crank and reducing the velocity of the numeral dials". End of citation. It is followed by three more points. The numbers in brackets refer to the drawing shown in Figure 7.

Figure 8 shows parts of the gear in a cut-away model. Because I didn't fully understand the cited line of the patent, I studied some more papers to find out the idea of the gear. Studying the open CURTA, the cut-away model and conversations with the constructors finally helped me to understand the idea.

The essence is that the setting gears on the driving members and the crown gears at their tops have five teeth (see Figure 8 and 9). On the other hand, the gears on the numeral dials have ten teeth. This unveils what the cited patent meant by "extends the time of engagement of the stepped drum with the setting gears". To transfer a nine, the driving member, which consists of a shaft, a setting gear, a tens-carrying gear and a crown gear, makes almost two complete turns. The Figures 8 to 11 show the described, and other, details.

As already said, apart from the two main German patents, there were many additional patents in Germany and all over the world. As an example for all of them, I give the patent claim of the significantly younger swiss patent from 1950: "Calculator for all four arithmetical functions with only one stepped drum and setting and counting members arranged in a circle around it, characterized by having setting and tens carrying gears with five teeth each and having a transmission between setting gears and numeral dials with a gear in such a way that the numeral dials make a tenth of a complete revolution per tooth of the stepped drum." It continues with 9 (!) additional claims.

Second part: the construction and operation of the CURTA

Changes in construction details of the CURTA

I already mentioned in the first part of my contribution [10] that the CURTA hasn't been modified much of a few decades. All this time (1947 to 1970) there were only two models, the 11-digit CURTA I and the 15-digit CURTA II. In contrast, the most famous German calculator, the MERCEDES-EUKLID, was put at the market in 21 (!) models. [11]

For the CURTA, and I will restrict myself to the CURTA I, it is really difficult to find constructive differences. However, there are some. I will comment on changes in the case, the setting knobs, the zeroizing lever and the crank.

Case

For the early models the top of the case was screwed onto the base with a normal, right-turning thread. For later models there is a left-turning thread. I asked Curt Herzstark why it was changed. Here is his answer:

"When screwing on the top it was possible that the crank would also turn a little bit to the right. This caused the machine to be not ready for use. There were several locks that prevented it. To release these locks one had to turn the crank until it came back to its resting position. This was not only laborious but also annoying. The left-turning thread prevent this source of errors - the crank cannot be turned left anyway." Indeed, a small turn of the crank is enough to block further operation of the machine. The real purpose of the locks engaging in such a manipulation is to prevent operator errors. Several locking mechanisms had already been protected by patents in an early stage, showing their significance. I won't go into details here.

Curt Herzstark told me another nice story about the case. During a visit to the CONTINA AG, Prince Heinrich of Liechtenstein brought a leather case he had been letting made for the CURTA. "Such a delicate machine has to be cuddled snugly, the tin case is much too rigid.", he said. Director Herzstark wanted to see the thing more closely. When handing it over, the machine almost fell to the ground because the leather top cover became loose. This took care of that new idea. During some time the tin cases were replaced by plastic ones. According to Curt Herzstark they didn't meet the requirements, so one returned to the tin cases. That's why nowadays it is the final aim of any calculator collector the possess a CURTA in a tin case with a normal thread !

Figure 12 and 13:Counter ring with setting shafts and the setting numeral dials connected to them. Clearly seen are the two versions of the setting knobs, before and after the end of 1948, and the identical way they run in the spiral groove.

Setting knobs

In the patent drawings (see Figure 7, backup 1/89) show cylindrical pins attached to the setting slides. In the early production they were made this way. Later [12] the shape of the setting knobs was changed, the difference is shown in Figure 12 and 13. When looking at both pictures one sees that the bearing of the setting slides has not changed, although there has been 15 years between the two machines shown. A screw-shaped groove, in which glide a bronze guiding screw and a steel ball, transforms a vertical movement in a rotation. The speed [12a] of the groove is exactly ten times as big as the distance traveled by the setting slide when displaced over one unit. Hence such a displacement turns the numeral dial that is connected to the setting shaft to the next number. The balls have a diameter of only 2 mm and are pressed by springs into the cavities that are visible in the pictures. This stops the slide at each number and allows for accurate setting (see also Figure 17).

I wanted to know from Mister Herzstark why they changed the setting knobs. He told me: "Originally I believed one should be able to see the numbers to which the slides were moved. That called for a setting knob that was as thin as possible, so it would cover the numbers as least as possible. Later we found out, one'd better concentrate on the numeral dials. This allowed for a more finger-friendly design of the setting knobs." [12b]

Zeroizing lever

It occurred often that the ring of the zeroizing lever (see Figure 14) broke off. Because the machine is round it could easily roll off the desk when not used carefully. Originally, the machine had to be disassembled to replace the lever. To avoid this, the zeroizing lever was reconstructed in such a way that it could put mounted on the clearing plate from the outside, without having to take the machine apart.

Figure 14: At the left the early machine nr 4086 and at the right the later machine nr 63122 with their differently shaped cranks. The ring-shaped lever under the crank is the zeroizing lever. Below that is the clearly visible counter ring, which has to be pushed up and rotated one position during multi-digit calculations. To obtain a deep ribbing that doesn't slip the ring was cut and milled.

Crank

An exterior change was made for the crank. Originally it was round, but later on it got edges. Figure 14 shows the difference. It simplified the manufacturing and reduced costs. As I already told in a previous contribution, the CURTA cost about 450 Swiss francs in 1950. Converted to todays' currency it would have cost 1500 Swiss francs [13] a price which is higher than what collectors pay for it now. I expect that the collectors' price will increase, CURTA's become rarer and more sought after. In the 1950's, its price was really high for a four-function calculator, but not without reason. Manufacturing it was very complicated. For instance, a lot of the numbers were engraved. The counter ring was cut and milled. Undoubtably, the advantage of this elaborate production was an extremely high quality of the finished product. Indeed, even now it is hard to find a CURTA that doesn't work. This is not very common for precision equipment that has been standing still for decades. Any collector can tell you stories about it. Often enough he has experienced some anxious moments when cleaning a machine - everything blocked !

Figure 15: Some parts of the CURTA. In total the CURTA I consists of 687 parts, 139 of which are different. At the right the star of springs, used to prevent the counters from turning to far. Top left a setting shaft with setting slide and fork for shifting the setting gear. Below four segments of the complemented stepped drum for the numbers 1 to 4. Between these segments and the star of springs a numeral dial. The photographed scale indicates the size: each block is 1 centimeter.

Figure 16: The two bearings shown are part of the carriage and bear the main shaft. The label with the tolerance specification illustrates the high accuracy needed for manufacturing parts of the CURTA.

An interview with CURTA constructors

My acquaintance with Curt Herzstark also brought me into contact with the constructors of "the early days". I met the mechanics Arnold Kessler and Hans Künzli [14] and could ask them some questions.

Which difficult constructive problems had to be solved, and how were they solved?

Künzli: "One problem I worked on for a long time was the construction of the stepped drum (final design see Figure 3). First I tried to mill and lathe some out of a aluminum block. Although I succeeded, I had to agree that the method was much too elaborate to be used in mass production. After some brainstorming the idea emerged to use die-cut parts (Figure 15). This way we could use abrasion-resistant steel. The only problem was the tolerances. The stepped drum consists of 37 segments [15] - a positive tolerance of only a hundredth of a millimeter already leads to a stall. For subtractions the stepped drum has to be pulled up only 3 mm. The mentioned positive tolerance adds up to one-eighth of this displacement - so it couldn't work. For a first series of 6 prototypes the segments had to be ground to their prescribed size. Even then, only 2 machines of this series worked. The second series was better - 4 out of 6 worked. Later we found the solution. Each segment had to be bent a tiny bit and have a negative tolerance. By pressing the segments together more or less we could force the stepped drum to its prescribed size."

Figure 17: Setting slide with setting shaft. The spiral groove is shown, that guides the little bronze screw, as well as the shallow cavities the rest the small ball. The slide can be halted at each position corresponding to a number.

Kessler: "It was extremely difficult to mill the spiral groove in the setting shafts (Figure 17). The tools we used wore extremely fast. There were no tools out of hardened steel for these small dimensions. Not only the wear of the tools bothered us, also the surface roughness of the groove. With a special drilling oil we succeeded finally to make grooves with the right roughness. When in use, the movement of the sliders had to be smooth, without jumps. Lubrication was out of the question. Tests showed that dust and oil soon formed a kind of resin. Finally we found a solution that didn't require any maintenance - the little guiding screw had to made of bronze. This ensured smooth sliding over the steel surface. Similar problems with wear showed up for the reset cam of the tens-bell (Figure 18). After several trials we finally found the right chrome plating."

Figure 18: Tens-bell with at the very bottom right the reset cam. Left from it a carrying lever made from chrome plated steel. A pin on the numeral dials shifts down the carrying lever. When the tens-bell, which is rigidly connected to the crank, is rotated, it pushes back the carrying levers and the carrying gears they operate (see also Figure 24 to 26)

Figure 19: A opened and a cut-away model, both with the finger-friendly setting slides. At the right of both machines the reversing knob is visible. Sliding it down makes the revolution counter count additive revolutions negatively. This can be useful in a lot of calculations.

Figure 20: The manufacturing building of the CONTINA AG in Mauren, Principality of Liechtenstein, to where the company moved in 1948. Picture from 1952.

Why were the numbers engraved in the numeral dials, and not printed ?

Künzli: "The numeral dials were anodized black. The numbers had to be clearly visible, that's why there were engraved after the surface treatment. The anodization posed a typical problem. In the beginning, the layer thickness was too large, which resulted in problems during operation."

You have told that the counter ring was cut and milled. What was the reason for this elaborate method ? Were there no simpler and cheaper methods ?

Kessler: "Indeed, those methods existed. But this part had to pushed up and rotated a decade for each multi-digit calculation. This required that the ring shouldn't slip in any case, even after years of use. The simple process of "randrieren" [15a] was out of the question, it couldn't be done deeply enough."

Figure 21: The first presentation of the CURTA at the Basel Trade Fair in 1949. In the center the inventor Curt Herzstark, at the very left Hans Künzli. The other gentlemen are (left to right): von Gerlicy, Asal and Maier.

Figure 22: A "sample suitcase" that was used when visiting customers to explain technical details. It contains: an open model, below which a carriage without clearing plate, above the name tag a complemented stepped drum and at the very top a lower main casting with its many holes to accommodate the transmission and setting shafts. One can find it at the bottom of a complete machine. At the right there are two setting slides, two transmission shafts and two main shafts. At the right bottom the so called machine body.

Which is the the nicest experience you remember related to the development of the CURTA ?

Kessler: "The service manual that I could produce. And the first presentation of the CURTA at the Basel Trade Fair in 1949 (see Figure 21). It was very exciting to share my enthusiasm for the machine with the people crowding around the booth. There were many professors, surveyors and teachers who wanted to know every detail - though the teachers usually didn't buy anything." Künzli: "Yeah, selling at trade fairs, we enjoyed that. Especially in the beginning it was not a thing we could count on. There were some dark periods."

Please tell !

Künzli continued: "For instance the rejection of a very large American order. At the Basel Trade Fair in 1949 an American came to the booth and wanted to order 10000 CURTA's [16] for retail in American department stores. This went beyond my competence so I called the manager of the Financing Society. He simply rejected, saying that the CURTA could only be sold in specialized shops."

The Principality of Liechtenstein didn't have any qualified precision mechanics after the second world war. So the CONTINA AG tried to attract mechanics by advertisements in the swiss daily journals. Mister Künzli responded to one of those advertisements in the Neue Züricher Zeitung. During his job interview he was told he could also bring his wife because the firm needed a secretary. That's how Hans and Paula Künzli became two of the four first employees of the CONTINA AG and made a significant contribution during the first pioneering years. Mrs. Künzli, which events from this pioneering time do you remember ?

Mrs. Künzli: "The start at April 1, 1947 with wild plans and the contrasting reality: production started in the ballroom of the Hirschen Hotel in Mauren, there were only the four of us. After that a nice period started: the expansion until 1951, when a conflict arose between the Financing Society and Curt Herzstark. It was around Eastern 1951. One fine morning the postmaster told he was not allowed to hand me the mail. Mister Herzstark was denied access to the factory. It came as a cold shower for me. I already had had the impression that the Financing Society would give our director Curt Herzstark more troubles than support. But I didn't expect they would go that far."

Figure 23: Manufacturing room of the CONTINA AG in 1951, Curt Herzstark is making an inspection tour (standing at the rear left).

An explanation of this incident.

From early on, the Financing Society had financial problems, for obvious reasons. By selling new shares the CONTINA AG had to be put to a sound financial basis. This meant that all old shares completely lost their value. Also the significant part owned by Curt Herzstark. Obviously, he didn't agree, which lead to the conflict mentioned above. Aided by a eminent patent attorney from Zürich the loss of patent rights could be prevented. Despite of that, Curt Herzstark worked only a few more years for the company as a free-lance consultant.

My interview had not come to an end yet. We talked extensively about the relation between the people of Liechtenstein and the swiss craftsmen. The relation was not good, on the contrary. In a public speech someone demanded "... to educate our people as fast and thorough as possible ... so we can get rid of the Swiss." On the other hand, the relation between the employees and technical director Herzstark was superb. I remember the words with which Curt Herzstark gave me the addresses of the interviewees: "Arnold Kessler and Hans and Paula Künzli, you have to talk with them. Without their help the CURTA could not have become what it is" and he added laconically, "they were great guys !"

Figure 24: A partially disassembled CURTA I. Exposed are some transmission shafts and two carrying levers, that are operated by the numeral dials above them and slide the tens-carrying gear down within reach of the tens-carrying tooth, that lies above the revolution counter toothing, but just can not be seen in the picture. On the other transmission members one cane see setting gears.

Figure 25: Disassembled carriage seen from below (left) and the machine body (right) which is mounted below the carriage in the complete machine. Two tens-carrying levers can be seen.

Figure 26: The same machine body as in Figure 25, photographed from below. A tens-carrying gear, that can be shifted along the transmission member, is shown slid down.

Figure 27: The "business card" of the CURTA, the bottom of the machine with the serial number, from which the collector can deduce the year of production.

The tens-carrying mechanism of the CURTA

The description of this ingenious construction is a must. Space limitations restrict me here to showing only a few pictures. I hope Figure 18 and 24 to 26 show enough details to clarify at least the principal idea to the interested reader. Maybe its description will be given in another contribution, or a future book. Maybe another reader will pick up the thread and publish his own contribution.

I don't know if I succeeded in completing the task Curt Herzstark gave me "to preserve my intellectual heritage". Surely I will never forget my encounter with the CURTA, its inventor and its constructors. I hope these two publications entice the reader not to forget the CURTA either. I also made some new contacts. These and the many responses are both a reward and an incentive. An incentive to continue my involvement with historical calculators. Maybe you, dear reader, can help me with that. I'm looking forward to your response.

Literature used:

P. Kradolfer: "Einige Rosinen aus der Entwicklung der Rechenmaschinen" [A few highlights from the evolution of calculators] Saarlander Aarau, 1988
K. Holecek: "Neue konstruktive Wege in Rechenmaschinenbau" [New design methods in the construction of calculators] Speech at October 19/20, 1950, published as a special edition of the "Heft Feinwerktechnik", Volume 55, June 11, 1951.
W. Lind: "Büromaschinen" Part 1, C.F. Winter'sche Verlagshandlung Füssen, 2nd edition, 1954.

Notes:

1: Peter Kradolfer, dipl.Ing. ETH SIA and technical high school teacher, Innerbergstrasse 27B, CH-3044 Ingerberg.
2: See backup 6/88 page 5 and backup 1/89.
3: Leibniz (1646-1716) constructed since 1671 four-function calculators with stepped drums as a central driving element; Since 1874, Odhner (1845-1905) made in St. Petersburg machines that were driven by pin-wheels, i.e. gears with a variable number of teeth. For details, see Literature, for instance, [1, p.3]. Multiplicating machines are not mentioned here, see [1, p.32].
4: Wilhelm Schickard (1592-1635) is nowadays regarded as the first inventor and maker of a four-function calculator with tens-carrying. He made his machine in 1623. Blaise Pascal (1623-1662), who has been regarded as the first inventor of a calculator for a long time, constructed an adding/subtracting machine with automatic tens-carrying in 1642.
5: For the number circle: see [1,p.27], for the mathematical proof, see [2, p.2].
6: There is also a brochure in A6 format with examples.
7: The TIM is a stepped drum calculator that was made in the 1930's by Ludwig Spitz & Co. GmbH in Berlin.
8: Production was started at April 1, 1947. In 1966 CONTINA AG was bought by the firm HILTI AG in Schaan. The CURTA was produced until November 1970.
It was sold until early 1973, after that it became silent around the mechanical miracle, nowadays it has become a collectors item.
9: D.R.P. means Deutsches Reichspatent. The designation Deutsches Reich was used for Germany from 1871 to 1945. The exact title of the patent is: Reichspatentamt, Patentschrift Nr. 747073 "Curt Herzstark in Wien. Rechenmaschine mit einer einzigen von Einstellrädchen umgebenen Staffelwalze" [Calculator with a single stepped drum surrounded by setting gears].
10: see also backup 6/88: Curt Herzstark and his calculator CURTA. Part 1; page 5ff and backup 1/89 page 6ff and 2/89 page 6ff.
11: An overview can be found in E. Martin: Die Rechenmaschine and ihre Entwicklung [The calculators and their development], 2nd edition, 1936 page 433ff. The Mercedes Euklid is a four function calculator with a proportion-lever and a construction of Chr. Hamann, Berlin. Its detailed description will be found in a later contribution.
12: since November 1948.
12a: [AdM: I mean the axial distance corresponding to one complete turn of a screw, my dictionary doesn't give me a clue of how to call it in English, I use a literal translation of the Dutch term here, which I feel is closer to English than the German one]
12b: [AdM: a close look at Figure 7 shows that in the very original version no control dials were provided: the shaft 7 just contains a sawtooth, not a spiral groove, and doesn't seem to be able to rotate; I don't see the control dials and I don't see a hole to look at the (eventual) control dials.]
13: According to the Swiss National Bank 100 swiss francs of 1950 are equivalent to 334.90 swiss francs in 1988.
14: Arnold Kessler (born 1926) worked from November 1948 until 1952 as a mechanic in the Contina AG; now he lives in St Antoni. Hans Künzli (born 1921) worked since the start of production at April 1, 1947 until 1951 as testing mechanic for the CURTA; his wife Paula was the first secretary at the same time; the Künzli couple now lives in Hergiswil.
15: Only the toothing for the main counter, without the 7 segments for the revolution counter.
15a: [From Gernot Hilger <gernot.hilger(at)netcologne.de> This is a south German/Swiss expression for Rändeln, which is knurling. You will be familiar with the process.]
16: Production in 1949 about 300 to 400 per month; in 1952 about 1000 per month.

Note: From Jürgen Müller: When I first came across the article on your web site, I was curious to find out more about "Backup" magazine, hoping it might contain more information on historical calculators. It was hard to track down, considering the very common title word... I found a copy at local teacher's library. Turned out that "Backup" was aimed at high school teachers of computer science. It was mostly concerned with fundamental algorithms and programs for then-modern microcomputers, but had a few articles on the history of computing (often by Peter Kradolfer). Hence, it's not too significant a resource for calculator fans. Nevertheless, here's the full bibliographic data I found:

Title: Backup -- Informatikzeitschrift für Schule und Weiterbildung. Publisher: Sauerländer Verlag, Aarau, Switzerland Available issues: 1.1986 - 5.1990 ISSN: 0258-4891

I did have some second thoughts about copyright. While the "Backup" magazine has faltered in 1990, after just a few years of publication.

The Calculator Reference by Rick Furr (rfurr@vcalc.net)

Back to The CURTA Calculator Page

Back to The Calculator Reference